ScienceBits
Lente Gábor blogja
Modern jóslatok a periódusos rendszerben
MAGYAR KÉMIKUSOK LAPJA
A Mengyelejev és más tudósok által a 19. század közepén megalkotott periódusos rendszer széles körű elfogadásához hozzájáruló lényeges tényező volt, hogy a rendszerezési logika alapján korábban még fel nem fedezett elemek létezését sikerült megjósolni. A három legnevezetesebb ilyen jóslat az ekabór (szkandium), az ekaalumínium (gallium) és az ekaszilícium (germánium) tulajdonságainak előrejelzése volt: ezeket kísérletileg két évtizeden belül igazolták is. Természetesen nem minden jóslat volt ennyire sikeres, Mengyelejev például két, a hidrogénnél könnyebb elem létezését is feltételezte.
Az már akkor is világos volt, hogy a tudományos elméletek egyik lényeges tesztelési módja a belőlük levezethető új észlelések kísérleti igazolása (vagy éppen megcáfolása).
Noha a periódusos rendszer a hetedik periódus utolsó elemének elnevezése, vagyis 2015 vége óta a lezártság érzetét kelti, még mindig léteznek tesztelésre váró előrejelzések a fel nem fedezett elemek tulajdonságairól. A legismertebb jóslatok középpontjában az atommagok stabilitása, illetve az elektronszerkezet áll, ezekről ad rövid áttekintést ez az írás.
Az atommagok sajátságaival – mindenek előtt stabilitásával és felezési idejével – kapcsolatos elméleti előrejelzések sokkal nagyobb múltra tekintenek vissza, mint az elektronszerkezetiek. Éppen száz éve, 1919-ben jelent meg Richard Swinne (1885-1939) német fizikus gondolatmenete, amely szerint a kozmikus sugárzás egyik lehetséges forrása a 100-as és 108-as elemekhez kapcsolódik. Az első transzurán elemek előállításának idején az volt az uralkodó vélemény, hogy az atommagok stabilitásának a spontán maghasadás jelensége szab majd felső határt, s emiatt 1939-ben az előállítható legnehezebb elemnek a 104-es rendszámút gondolták, néhány évvel később pedig a 108-ast.
A magstabilitási elméletekben manapság is jelentős szerepet játszanak a mágikus számok, amelyekhez kiemelkedő magstabilitás tartozik (2, 8, 20, 28, 50, 82 és 126). A ma ismert legnehezebb stabil izotóp az ólom-208, amelyben a protonok (82) és neutronok (126) száma is mágikus. (2003-ig a bizmut-209-et gondolták a legnehezebb stabil izotópnak, ekkor azonban kiderült róla, hogy alfa-bomló, a felezési ideje 2×1019 év.) Mára nagyon valószínűvé vált, hogy a neutronok és protonok 100-nál nagyobb mágikus számai különböznek, de a szakértők között nincs teljes egyetértés arról, hogy melyek is ezek. Így aztán a várható magstabilitásokról is széles skálán mozognak az előrejelzések. A legtöbbet idézett jóslat az, hogy a 298Fl-izotóp (flerovium, 114 proton és 184 neutron) körül kiemelkedő stabilitású atommagok találhatók majd, ez lesz a "stabilitási sziget". A sziget csúcsán lévő izotóp akár stabil is lehet, de felezési ideje majdnem minden előrejelzés szerint meghaladja az egy évet. Ez a sziget látható az alábbi ábrán. A 291Cn (kopernícium) és 293Cn izotópokat is gyakran említi a szakirodalom a kivételes stabilitásúak között. Egy kisebb stabilitási maximum ("stabilitási szikla") a 272Ds (darmstadtium) közelében is várható.
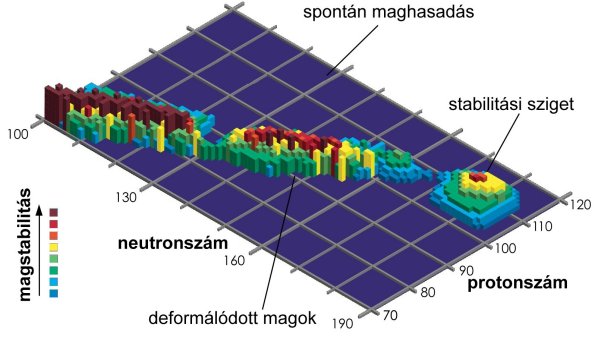
Noha a jóslatok megszületése óta ezeket az elemeket már előállították, egyelőre csak a stabilitási szigethez képest lényegesen kisebb tömegszámú izotópok ismeretesek. Az előrejelzések azonban sokkal tovább mennek: további stabilitási szigetek várhatók a 342Ubh és 354Ubh (unbihexium, a 126-os rendszámú elem), illetve a 472Uhq és 482Uhq (unhexkvadium, a 164-es rendszámú elem) környezetében. Ezen atommagok spontán hasadása valószínűleg nagyon lassú, és alfa-bomlásuk felezési ideje is meghaladja az egy évet.
Kevésbé nyilvánvaló, hogy az atomok elektronszerkezetének leírásában egyáltalán van-e helyük jóslatoknak. A Nobel-díjas Glenn T. Seaborg 1996-ban megjelent, a periódusos rendszerről szóló cikkében egyszerűen csak folytatta az eddig megismert elveket, és a nyolcadik periódusba így összesen 50 elemet helyezett egymás után. Az 5g és 6f pályák betöltésével keletkező 32 tagú elemcsoportot szuperaktinidáknak nevezte. Ezt a gondolatmenetet folytatva 2002-ben h, i, j és k pályák figyelembe vételével az elemeket 1138-as rendszámig feltüntető periódusos rendszer is született, ez látható a következő ábrán:

Elméleti számításokból azonban meglehetősen nagy bizonyossággal kiderült, hogy már a hetedik periódus végén is figyelembe kell venni a relativisztikus hatásokat, mert az elektronok mozgási sebessége a fénysebességhez közelít; a nyolcadik periódusban pedig ez az effektus nagyon is lényegessé válik. Az ilyen számításokat a legrészletesebben Pekka Pyykkö finn kémikus végezte el. Az eredmények szerint a p pályák degeneráltsága ilyen nagy rendszámok esetében megszűnik: az energiaszint az egy pályát tartalmazó p1/2 és a két pályát tartalmazó p3/2 csoportra hasad fel. Ilyen hatások következménye az, hogy a 114-es rendszámú flerovium kémiai tulajdonságai a jóslatok szerint inkább emlékeztetnek a nemesgázokéra, mint a fölötte lévő ólomra vagy az ónra. A 8p és 9p pályák esetében ez a felhasadás már olyan jelentős, hogy a 9s és a 9p1/2 pályák energiája is a 8p3/2 szintje alá kerül, így a pályák energiabetöltési sorrendje a következőképpen alakul:
8s < 5g ~ 8p1/2 < 6f < 7d < 9s < 9p1/2 < 8p3/2
Ennek a következménye az, hogy ha a periódusos rendszerben továbbra is az azonos vegyértékelektron-konfigurációjú elemeket akarjuk egy csoportba (vagyis egymás alá) írni, akkor a rendszámok már nem növekedhetnek monoton módon. A periódusos rendszer egy, a megjósolt elektronkonfigurációkat tükröző, Pekka Pyykkö által javasolt kiterjesztését mutatja be az alábbi ábra. A rendszámok monoton növekvésének megtörésével egy érdekes történeti párhuzam húzható: 1869-ben Mengyelejev az atomtömegek sorrendjébe állította az elemeket a periódusos rendszerben, de ezt a szabályt fel kellett rúgnia a tellúr és a jód között ahhoz, hogy a rendszer valóban a kémiai sajátságokat tükrözze.
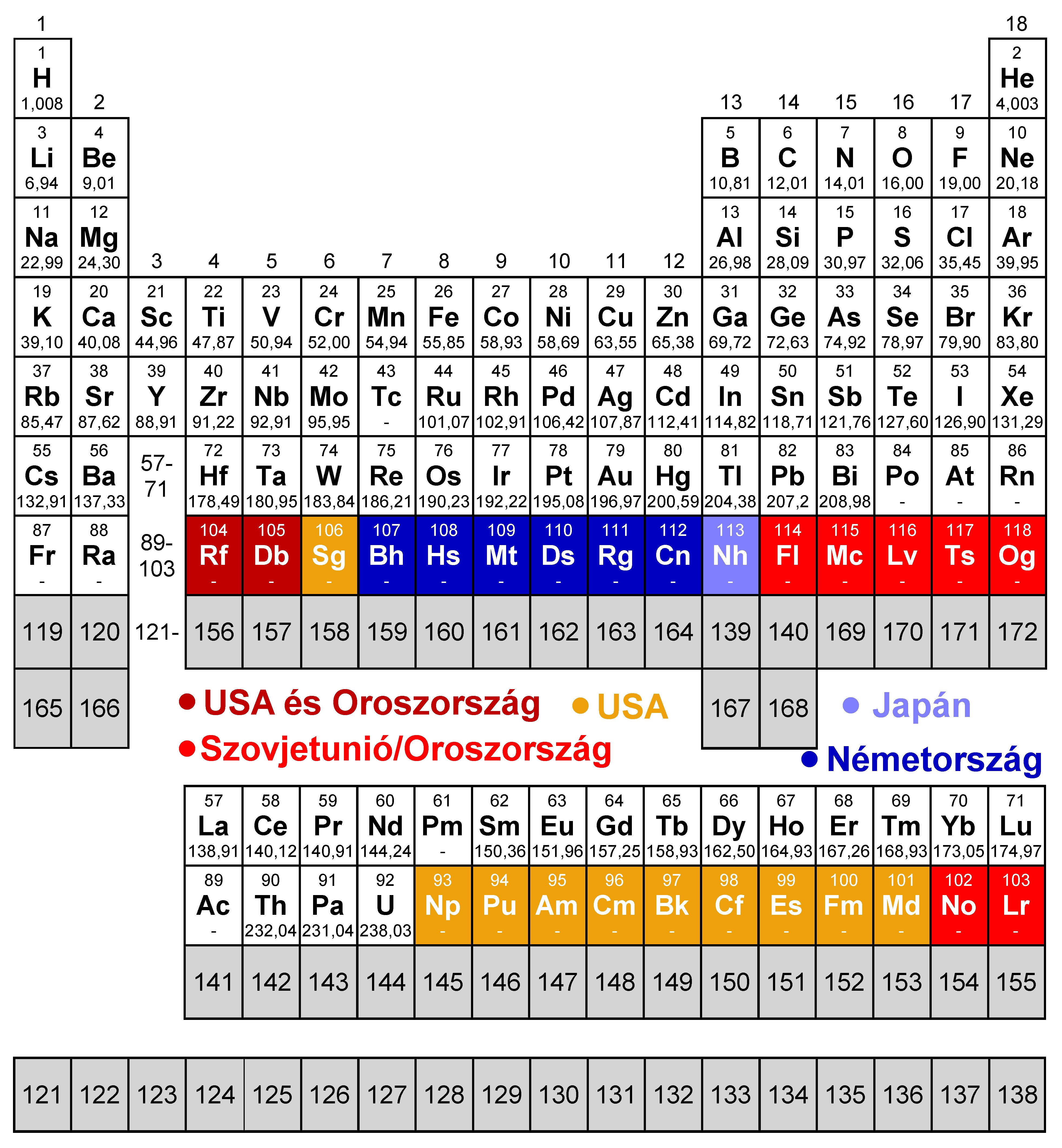
Az elektronszerkezet kvantummechanikai leírásának egyéb furcsaságai is vannak. A 118-as rendszám fölött például a probléma leírására szokásosan használt egyenletben megjelenik egy második megoldás, majd 137-es rendszám környékén az energia értékére képzetes számok is lehetségessé válnak. A legelfogadottabb jelenlegi elméletek azt is jósolják, hogy a 172-es rendszám fölött a Schrödinger-egyenletnek már nem lehet még rövid időtartamra stabil megoldása sem: ekkor az elektronok és az atommagban lévő protonok neutronná egyesülése dominánssá válik. Így könnyen meglehet, hogy a peridusos rendszer elvi végét nem a magstabilitás, hanem az elektronszerkezet sajátságai határozzák majd meg.
Sajnos igen valószínűtlen, hogy a periódusos rendszerhez kapcsolódó modern jóslatokat az elkövetkező két-három évtizedben kísérleti adatokkal lehetne összevetni. A szupernehéz elemekből rendszerint néhány atomot állítanak elő, ebből spektroszkópiai módszerekkel az elektronszerkezetre következtetni reménytelen vállalkozás, kémiai sajátságokat meghatározni pedig még inkább az. A stabilitási sziget kísérleti megtalálására sincsenek reális elképzelések. Noha a flerovium elemet előállították már, a sziget várható középpontja a 298Fl-izotóp lenne, a legnehezebb ténylegesen előállított izotóp tömegszáma viszont még csak 289. A stabilitási sziget körüli ismert izotópok felezési időit foglalja össze a következő táblázat. Látható, hogy a meglévő adatok extrapolálásába könnyen beleképzelhető a stabilitási sziget létezése: a Fl jelenleg ismert izotópjainak felezési ideje például monoton növekszik a tömegszámmal:
| P R O T O N S Z Á M | |||||||
| 110 | 111 | 112 | 113 | 114 | 115 | ||
| N E U T R O N S Z Á M | 157 | 267Ds 0,003 ms | |||||
| 158 | |||||||
| 159 | 269Ds 0,23 ms | ||||||
| 160 | 270Ds 10 ms | ||||||
| 161 | 271Ds 0,21 s | 272Rg 2 ms | |||||
| 162 | |||||||
| 163 | 273Ds 0,17 ms | 274Rg 12 ms | |||||
| 164 | |||||||
| 165 | 277Cn 0,69 ms | 278Nh 1,4 ms | |||||
| 166 | |||||||
| 167 | 277Ds 3,5 ms | 278Rg 4 ms | |||||
| 168 | 279Rg 90 ms | ||||||
| 169 | 279Ds 0,18 ms | 280Rg 4,6 s | 281Cn 0,18 s | 282Nh 73 ms | |||
| 170 | 280Ds 6,7 ms | 281Rg 17 s | 282Cn 0,91 ms | 283Nh 75 ms | 284Fl 2,5 ms | ||
| 171 | 281Ds 9,6 s | 282Rg 100 s | 283Cn 4,2 s | 284Nh 0,91 s | 285Fl 0,10 s | ||
| 172 | 283Rg 5,1 min | 284Cn 98 ms | 285Nh 4,2 s | 286Fl 0,12 s | 287Mc 37 ms | ||
| 173 | 285Cn 28 s | 286Nh 9,5 s | 287Fl 0,48 s | 288Mc 0,16 s | |||
| 174 | 286Cn 8,5 s | 287Nh 5,5 s | 288Fl 0,66 s | 289Mc 0,33 s | |||
| 175 | 286Rg 11 min | 289Fl 1,9 s | 290Mc 0,65 s | ||||
| 176 | 290Fl 19 s | ||||||
| 177 | 290Nh 2 s | ||||||
A szigethez tartozó izotópok előállítását az akadályozza, hogy a stabilis atommagokhoz a rendszám növekedésével egyre nagyobb relatív neutronfelesleg szükséges. A jelenlegi kísérletekben két kisebb atommag hideg fúziójával állítják elő a szupernehéz elemeket – ilyen módon a kívánatos neutron/proton arányt lehetetlen elérni. A magfizikai egyik kedvenc atommagja a 48Ca-izotóp, amely stabil, a természetes kalcium 0,187%-a, és a protonok számához képest meglepően sok neutron van benne. A 297Og-izotópot (ognanesszon) például 249Cf (kalifornium) és 48Ca (kalcium) ütköztetésével állították elő. A 119-es rendszámú elem (Uue) előállításhoz a kalifornium helyett egy einsteinium-izotópot kellene ugyanilyen kísérletben céltárgyként használni, de ehhez semelyik laboratóriumban nem sikerült még elég nagy mennyiség einsteiniumot előállítani. A dubnai Flerov Laboratóriumban 2019 elején kezdődtek el a próbálkozások arra, hogy 48Ca helyett az 5,18% természetes gyakoriságú, ugyancsak stabil 50Ti izotópot használják. Sajnos ennek az atommagnak az elméletek szerint kedvezőtlenebbek a magfizikai tulajdonságai, így a 48Ca-nál jóval kisebb valószínűséggel vesz részt hideg magfúzióban, de azért van remény arra, hogy néhány éven belül beszámoljanak majd a 119-es (Uue, ununennium) és 120-as (Ubn, unbinillium) elemek előállításáról is.
![]() 2019.12.01.
2019.12.01.
