ScienceBits

Még távolabb a napvitorla

TUDOMÁNYOS? FANTASZTIKUS!

Nemrég jelent meg egy kicsit hosszabb írásom a napvitorlázásról a Természet Világában, majd ezen a blogon is. Azóta az eredeti cikkben megjelentekhez képest jelentős változások történtek. Ezek akár megtévesztőek is lehetnek: a 2015-ben végrehajtott sikeres tesztet akkor még LightSail-A-ként emlegették, de a nevét visszamenőleg LightSail-1-re változtatták. Így persze az eredeti LightSail-1-et is át kellett nevezni (ennek fellövését tavaly nyáron még 2016 áprilisára, tehát épp mostanra tervezték), ebből lett mára a LightSail-2. A szondaindítást pedig majd egy évvel, 2017 márciusára halasztották el.

Szintén azóta történt, hogy a Planetary Radio egyik adásában (ezeket a LightSail kísérletek gazdája, a Planetary Society készíti) hallottam arról, hogy a napvitorlázás révén egy trükkel akár a Naprendszert viszonylag hamar elhagyó űrszondát is lehetne építeni. Az ötlet az, hogy nagyon meg kell közelíteni a Napot, így − még ha rövid ideig is − elég nagy gyorsító erőre lehet szert tenni.

Hasonló "trükkökről" már halottam: például a bolygók megfelelő időpontban és szögben való megközelítése jelentősen felgyorsíthat egy olyan űrszondát, amely a Naprendszer külső része felé tart. Ezt gravitációs hintamanőverként is szokták emlegetni, és az érdekessége az, hogy időnként még akkor is érdemes a Nap (pontosabban a Vénusz vagy a Merkúr) felé elindulni, ha egyébként távolodni akarunk tőle.

Így aztán végeztem is néhány modellszámítást a napközeli pálya hatásának felmérésére. Az űrszonda ugyanaz volt, amelyet az előző írásomban már feltételeztem: a tömege 1000 kg, a napvitorla felülete 100.000 m², a vitorla beállítási szöge pedig ideális, vagyis éppen merőleges a szonda mindenkori sebességének és a tőle a Naphoz húzott egyenes által bezárt szögnek a felezőjére. A Planetary Radio említett adásában arról volt szó, hogy a pálya napközeli pontjának Naptól mért távolsága a Merkúr pályasugarának egytized része körüli kell hogy legyen, ami 7 millió kilométer. Ezért úgy terveztem meg a Föld pályájának elhagyását, hogy a szonda sebességének nagyságát (kb. 30 km/s) nem, csak az irányát változtatjuk meg megfelelően; ez tűnt a legtakarékosabb lehetőségnek. Útban a Nap felé a vitorla csak akadály lenne, ezért annak a kinyitását éppen a napközeli pontra időzítettem.

Igen érdekes eredményeket számoltam. Egy ilyen pályán haladva a szonda 36 nap alatt eléri a Naphoz legközelebbi pontot. Ekkorra a sebessége 114 km/s-ra növekszik. A visszaút a Föld pályájáig a Napvitorla gyorsító hatásának köszönhetően már csak 17 napig tart, vagyis az 53. nap után már tényleg kifelé tartana, a sebessége ekkor 93 km/s lenne. Ez a napvitorla nélküli űrhajózásban eddig elképzelhetetlen lehetőségeket jelent: a Jupiter pályáját a küldetés 134. napján keresztezi a szonda a Szaturnuszét pedig a 220. napon. A szonda simán túllépné a Naprendszer elhagyásához szükséges szökési sebességet, a végén kb. 86 km/s-mal már majdnem egyenes vonalban távolodna a Naptól, és szűk két év alatt a Neptunusz pályáján kívülre jutna. Összehasonlításként: a gravitációs hintamanővert egyébként nagyon hatékonyan felhasználó New Horizons űrszondának ugyanehhez mintegy nyolc év kellett. A kiszámolt pályát a következő ábrán a kék görbe mutatja:

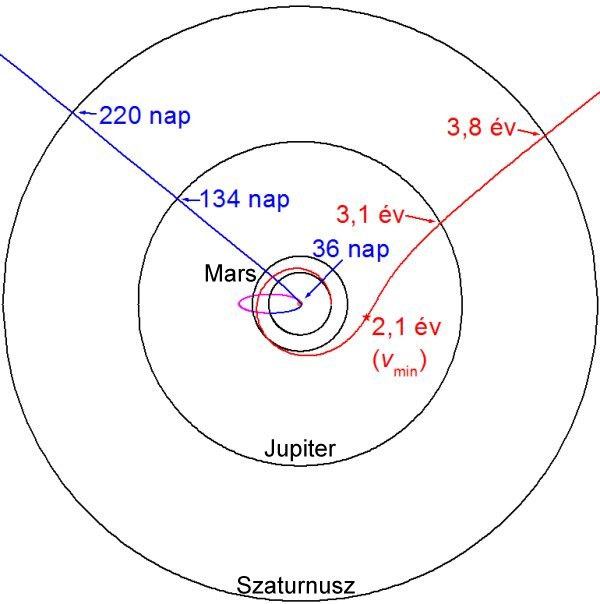
Elméleti napvitorlázási pályák a Naprendszerben.
1000 kg tömeg és 100.000 m² felületű napvitorla
(napsugarakkal ideális szögben),
A kék szonda pályája napvitorla nélkül,
Lézerrel hajtott, 1000 kg tömegű űrszonda

Persze ha alaposabban belegondolunk, közel sem ennyire rózsás a helyzet. A Nap sugara mintegy 700 000 km, vagyis ha a szonda a Nap középpontját 7 millió km-re megközelíti, akkor az egy csillag felszínétől már csak 6,3 millió km távolságban van. Igencsak jóféle szerkezeti anyagokból kellene készíteni, hogy az ezzel járó intenzív sugárzást (nemcsak fényt!) károsodás nélkül elviselje. Különösen a vitorla anyaga kritikus kérdés, hiszen ennek igen vékonynak kellene lennie ahhoz, hogy a saját tömege minél kisebb legyen.

Van egy másik probléma is. Ugyan a szonda Föld mellőli indításánál a sebességet nem kellene növelni, a sebesség irányán viszont kb. 73°-ot kellene forgatni. Habár (fizikai értelemben vett) munkavégzés ehhez elvileg nem szükséges, mert a sebességváltozást előidéző erő lehet mindig merőleges a sebességre, erőlökés (a ható erő megszorozva az idővel) valójában igencsak nagy kell egy ilyen manőverhez. Az ábrán a lila színű görbe azt mutatja, hogyan nézne ki ez a pálya napvitorla nélkül, amelyen a Marsig simán el lehetne jutni. Ha viszont ezt az erőlökést mind irányváltoztatás nélküli gyorsításra használnánk, a 30 km/s-os kiindulási sebességről egészen 70 km/s-ra lehetne gyorsítani a szondát! Ez pedig már önmagában is elég a Naprendszer elhagyásához; a Neptunusz pályáját két és fél év múltán keresztezné. Minek ide napvitorla?

Összességében az az érzésem, hogy a Nap közelében elérhető nagy gyorsulás fontos lehet, de a valóságban ennek a felhasználásához bonyolultabb műveletek sorát kell majd kitalálni és elvégezni. Például kezdetben lehetne a sebesség csökkentésére használni a napvitorlát (ez csak a szögbeállítás kérdése), aztán összecsukni és a Vénusz mellett elhaladva egy gravitációs hintamanőverrel sebességet is nyerve megközelíteni a Napot, itt pedig újra vitorlát bontani.

A Naprendszerben kifelé napvitorlázással az az alapvető baj, hogy a fénynyomás tolóereje a Naptól mért távolság négyzetével fordítottan arányos. Már több helyen olvastam arról, hogy a Földön üzemeltetett hatalmas lézerek felhasználásával is lehetne gyorsulni az űrben. Ekkor nagyméretű vitorlára sem lenne szükség, mert egy lézernyaláb széttartása nagyon kicsi. Persze „célozni” igen jól meg kellene tanulni. Ezt én úgy képzeltem el, hogy a lézert nem is a Földre, hanem a Merkúr pályájára építjük azért, hogy hatékonyabban üzemeltethessük napenergiával. Itt négyzetméterenként 6000 W teljesítményt lehetne nyerni: számításaim szerint 20.000 m² felületű napelem már elvileg akár 1 N tolóerejű lézert hajthat. Ha mondjuk 10% a konverzió hatékonysága, akkor is 200.000 m² elég az 1 N-hoz, a méretnövelés pedig itt nem probléma, hiszen a napelemeket nem kell mozgatni. Az ábrán a piros színű vonal mutatja be egy olyan, 1000 kg tömegű fényvitorlás pályáját, amelyet a Földről indítanak és a Merkúr pályáján lévő lézer hajt. Ez eleinte lassulva távolodna a Naptól. Az indítás után 2,1 évvel, az aszteroida-övezetben érne el kb. 14 km/s-os minimális sebességét, innentől viszont az 1 N tolóerő meghaladná a szondára ható gravitációs erőt, vagyis gyorsulni kezdene. A Szaturnusz pályáját szűk négy évvel indítás után keresztezné, de ekkorra már neki is elegendő mozgási energiája lenne a Naprendszer elhagyásához. A mozgás érdekessége, hogy az állandó tolóerő igazából nem a Nap, hanem a Merkúr felől jön, de minél kijjebb jutunk a Naprendszerben, annál kisebb a két irány közti különbség.

A két számolásnak van egy közös eleme: mind a kettőben olyan pályákat számoltam ki, amelyek megvalósítása rendkívüli technikai nehézségek megoldását feltételezi.

2016.04.15.