ScienceBits

Alien: újra nyomoz a KOBALKIVI

KÖZÉPISKOLAI KÉMIAI LAPOK, GONDOLKODÓ

Feladat:

A Kozmikus Baleseteket Kivizsgáló Intézet (KOBALKIVI) szakemberei külső megbízást kaptak a Weyland-Yutani Kereskedelmi Társaságtól a Nostromo és a Sulaco űrhajók szerencsétlenségének kivizsgálására, amelyekről A nyolcadik utas a halál és A bolygó neve halál című filmekben maradtak fenn adatok. Ellen Ripley mindkét baleset során robbanásszerű nyomáscsökkenést idézett elő azért, hogy az ellenséges szörnyet az űrbe juttassa. A Nostromo esetében ez az anyaűrhajó megsemmisülése után, a mentőkabinként használt űrkompban történt: Ripley űrruhát viselt, s a levegő a hátsó zsilip kinyitása után röviddel teljesen elszökött. A másik esetben Ripley a Sulaco rakodótéri zsilipkamráját nyitotta ki 68 másodpercre, közben űrruhát nem viselt. A történetek megerősítése céljából a KOBALKIVI szakembereitől a következő kérdésekre várják a választ:

1. Mennyi idő alatt csökkent a Nostromo űrkompjában a nyomás a kiindulási 1%-ára? (Ez nagyjából az az idő, amíg a szívóhatás tart.)
2. Mennyit változott a nyomás és a hőmérséklet a Sulaco belsejében?
3. A földfelszínen nagyjából milyen sebességű szélnek felelne meg a légáramlás sebessége a zsilipnyitás után?

A KOBALKIVI szakemberi kérdéseikre megkapták a szükséges technikai adatokat is. A Weyland-Yutani Kereskedelmi Társaság űrhajóiban a szokásos nyomás 93000 Pa, a hőmérséklet 21 °C. Az űrkompzsilipek standard mérete 110 cm ∙ 120 cm, míg a rakodózsilipeké 3,1 m ∙ 4,3 m. Az űrkompok szokásos felszállótömege 31,2 tonna, légtérfogata 435 m³. A Sulaco tömege a baleset idején 22700 tonna körül lehetett, az űrhajó légterének térfogata pedig 830000 m³.

A KOBALKIVI először a Googleplex szuperszámítógép segítségét kérte. Ő azt közölte, hogy nem ér rá ennyire könnyű, a kinetikus gázelmélet és elsőrendű folyamatok segítségével megoldható problémával foglalkozni, mert éppen az élet nagy kérdésére keresi a választ. Rövid idő elteltével azonban minden más magyarázat nélkül egy képlet jelent meg a legnagyobb képernyőn:

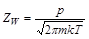
Mit válaszolt a KOBALKIVI a kérdésekre?

Megoldás:

A feladat megoldását logikusan a 2. kérdés hőmérsékletre vonatkozó részével kell kezdeni. A leírt körülmények között mindkét esetben az űrhajó belsejéből az űrbe, vagyis vákuumba szökik ki a levegő (a jelenség a tudományos szakirodalomban gyakran effúzió, termodinamikai tankönyvekben pedig ’gázkiterjedés nulla külső nyomással szemben’ néven szerepel). Ilyen körülmények között a hőmérséklet nem változik, vagyis a folyamat egyszerre adiabatikus (hőcsere nélküli) és izoterm (állandó hőmérsékletű). Egy kicsit mélyebb magyarázatot keresve: a kinetikus gázelmélet szerint egy gázminta hőmérsékletét a molekulák átlagos mozgási sebességéből egyértelműen meg lehet adni. Ha a gáz az űrbe szökik, akkor minden egyes molekula kiszökik, amely eltalálja az űrbe nyíló lyukat, függetlenül a mozgási sebességétől. Így a kiszökő molekulák átlagsebessége éppen megegyezik majd a benn maradó molekulák átlagsebességével, vagyis összességében a benn maradó gáz hőmérséklete nem változik.

Ezután az 1. kérdésre, illetve a 2. kérdés második felére azonos gondolatmenet alapján lehet válaszolni. A különbség csupán az, hogy az 1. kérdésben az ismert nyomáscsökkenéshez tartozó időt kell meghatározni, míg a 2. kérdésben az ismert idő alatt bekövetkező nyomáscsökkenést. A gondolatmenet kiindulópontja az a képlet, amelyet a Googleplex szuperszámítógép kiírt:

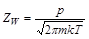
A képletet a kinetikus gázelmélet segítségével lehet levezetni. Ebben a képletben Z_W az egységnyi idő alatt egységnyi falfelületnek ütköző molekulák száma (ezt effúziós sebességnek is nevezik), p a gáz nyomása, m az egyedi gázmolekulák tömege, k a Boltzmann-állandó, T pedig a hőmérséklet. A kiindulási körülmények között a képlettel ki lehet számolni egy effúziós sebességet, a probléma csak az, hogy a folyamat során csökken a nyomás, így az effúziós sebesség is. Az űrhajó belsejében a gáz anyagmennyiségének változási sebessége (dn/dt) a következőképp adható meg az Avogadro-állandó (N_A) segítségével:

A levegőt az adott körülmények között ideális gáznak tekinthetjük. A hőmérséklet és a térfogat állandó, így az ideális gáz állapotegyenlete szerint a nyomásváltozás egyenes arányos az anyagmennyiség megváltozásával:

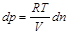
Ezt összevetve az anyagmennyiség változási sebességére vonatkozó korábbi egyenlettel a következő kifejezéshez jutunk:

Tehát a nyomásváltozás sebessége egyenesen arányos magával a nyomással. Erre utalt a Googleplex szuperszámítógép akkor, amikor válaszában elsőrendű folyamatokra utalt. Egy ilyen probléma megoldása mindig csökkenő exponenciális függvény, ebben az esetben:

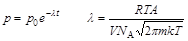
A λ állandó értékét mindkét kérdésben ki lehet számolni. Kicsit egyszerűsíthető a számolás úgy hogy a λ-ra vonatkozó kifejezés nevezőjében az Avogadro-állandót bevisszük a gyökjel alá, így egy molekula tömegének helyére a moláris tömeg, a Boltzmann-állandó helyére pedig a gázállandó lép. A levegő átlagos moláris tömege 29 g/mol. Az 1. kérdésben a felület 1,1 m ∙ 1,2 m, a térfogat pedig 435 m³, így λ értéke 0,351 s^-1. A 2. kérdésben a felület 3,1 m ∙ 4,3 m, a térfogat 830000 m³, így λ értéke 0,00186 s^-1. Az 1. kérdésben az idő így:

A 2. kérdésben a nyomás:

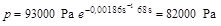
A harmadik kérdés arra vonatkozott, hogy a Sulacoban a zsilipnyitás után a légáramlás sebessége nagyjából milyen szélsebességnek felelne meg a földfelszínen. Vegyük észre, hogy ehhez a molekulák egyedi mozgási sebességének nincsen sok köze, mert a Földön szélcsendes időben is kb. 500 m/s sebességgel mozognak a levegőben lévő molekulák. A zsilipnyitás után egy a zsilipben elképzelt, A nagyságú felületre p_űh∙A nagyságú erő hat egy irányból (p_űh a nyomás az űrhajó belsejében). A földfelszínen szeles időben ugyanekkora erőt okozó v szélsebességet becsüljük meg Newton II. törvénye alapján, amely szerint az erő az időegységre jutó impulzusváltozás. Szél esetén Δt idő alatt A felületnek összesen AvΔt térfogatú, vagyis AvΔtρ tömegű levegő ütközik (ρ a levegő sűrűsége a földfelszínen). Ugyanennyi idő alatt a sebesség v-ről nullára csökken, tehát az impulzus megváltozása Av²Δtρ, az ehhez tartozó erő pedig Av²ρ. Ennek kell p_űh∙A-val egyenlőnek lennie, amiből a szélsebességre az ideális gáz állapotegyenletét is felhasználva a következő összefüggés vezethető le:

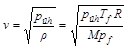
A képletben p_f a földi légnyomás, T_f pedig a földi hőmérséklet. Ezek közül p_f szokásos értéke 101325 Pa, T_f-re viszont nem ad közvetlen útmutatást a feladat, ezért vegyük az űrhajóban lévő levegő hőmérsékletével azonosnak (21 °C). Ezekkel az adatokkal számolva v-re 278 m/s, vagyis majdnem pontosan 1000 km/h adódik.

Kiegészítő gondolatok a megoldáshoz:

A megoldás végén néhány megjegyzés kívánkozik a versenyzők által beküldött néhány gondolathoz, illetve tipikus hibához is:

1. Az űrhajók tömegét megadta ugyan a feladat, de ezekre sehol nem volt szükség a számolásnál.
2. A moláris tömeg szokásosan használt mértékegysége ugyan g/mol, de szigorúan véve az SI-mértékegység kg/mol, a megoldásban leírt képletekben ezt kell használni. Aki nem végzett (legalább fejben) megfelelő dimenzióanalízist, az helyes képleteket használva is hibás számértékre jutott végeredményben.
3. Többen azzal indokolták a hőmérséklet változatlanságát, hogy az űrhajó tömege sokkal nagyobb a benne lévő levegőénél, s így az űrhajó anyagában tárolt hő gondoskodik az izoterm körülményekről. A megoldás korábbi részéből kiderül, hogy nem erről van szó. Ez a magyarázat azért is kétséges, mert ez irreálisan gyors hőcserét feltételez a szilárd és a gázfázis között.
4. Egy megoldó - helyesen - rámutatott arra, hogy a levegő keverék, azért az egyes komponensek különböző sebességgel szöknek, vagyis a folyamat során változik a gázfázis összetétele. Ha ezt figyelembe vesszük, s a levegőt 78:21:1 arányú nitrogén-oxigén-argon elegynek fogadjuk el, akkor a nyomásváltozást Dalton parciális nyomásokra vonatkozó törvényét is figyelembe véve a következőképpen kellene leírni:

   

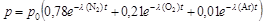
   A képletben a λ értékek a három különböző gázra a moláris tömegek eltérésének megfelelően különbözőek lennének. Ez a képlet csekély mértékben eltérő eredményeket ad a bemutatott megoldástól, de még az ilyen szempontból legrosszabb esetben, vagyis az 1. kérdésnél is az első három értékes jegyben nem okoz változást. Látványosabb a különbség akkor, ha a gáz összetételének változását figyeljük, mert az első kérdés körülményei között 930 Pa teljes nyomásnál a gázfázisnak már nem 1, hanem majdnem pontosan 2%-a argon. Ez viszont nem volt kérdés.

   Egyébként nem túl valószínű, hogy a jövő űrhajótervezői a levegő argontartalmának fenntartását fontos kérdésnek gondolnák, az eddig épített űrhajók légterében gyakran még nitrogén is jóval kevesebb van, mint a Föld légkörében. Az emberi kényelemérzet szempontjából a megfelelő páratartalomról, vagyis a vízgőzről való gondoskodás sokkal fontosabb feladat. 21 °C-on és 93000 Pa nyomáson a kellemes, 50%-os relatív páratartalom fenntartásához a gázelegy mintegy 1,3%-nak vízgőznek kellene lennie.

5. Többen az adiabatikus reverzibilis folyamatokra vonatkozó képlettel próbáltak meg számolni (pV^γ = állandó, ahol γ a gáz állandó nyomáson és állandó hőmérsékleten mért mólhőjének hányadosa). Egy ilyen folyamatban a külső nyomás folyamatosan változik, s mindig egyenlő a gázelegy teljes nyomásával (ettől reverzibilis). A pV^γ = állandó képlet használata ezekben a hibás megoldásokban nagyon bonyolulttá tette a levezetéseket, így az ebbe a zsákutcába betévedő megoldók sajnos sokat számoltak anélkül, hogy közelebb kerültek volna a végeredményhez. Adiabatikus reverzibilis körülmények között a nem nulla külső nyomás miatt a kiterjedéskor munkát kell végezni, s ezért a gáz hőmérséklete csökken. A feladat ugyanakkor vákuumba kiterjedésről szólt, ahol a térfogatnövekedés nem jár munkavégzéssel, vagyis a hőmérséklet sem változik.
6. A 2. kérdés nyomáscsökkenésre vonatkozó részét egy egyszerűsített gondolatmenettel is meg lehetett oldani. Ha valaki kiszámolta a Z_W értékét, s ezt megszorozta az eltelt idővel, akkor az anyagmennyiség-csökkenés elég jó becslését kapta, mert a folyamat közben a nyomás a részletes számolás szerint is csak 12%-ot csökkent, vagyis az ez által okozott sebességcsökkenést akár el is lehetett hanyagolni.
7. A 3. kérdés megválaszolásánál sokan hivatkoztak a Bunsen-féle kiömlési törvényre. Ez az összefüggés a feladatíró számára korábban ismeretlen volt, az Eötvös Loránd Tudományegyetem egyik hallgatói gyakorlatának leírásában megtalálható az Interneten (http://metal.elte.hu/~phexp/doc/fgm/e23s2.htm). Az itt található leírás szerint Δp túlnyomású tartályból egy kicsiny nyíláson keresztül ρ sűrűségű gáz v kiáramlási sebessége: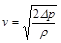

   

   Ezt vákuumba való kiáramlásra alkalmazva és az ideális gáz állapotegyenletét is felhasználva a következőképpen alakítható át:

   

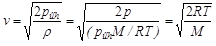
   Az így kapott képletben az űrhajóban lévő nyomás nem is szerepel, az eredmény egyértelműen az egyedi molekulák mozgási sebességével van kapcsolatban, nem a szélsebességgel. Egy gázmintában rengeteg molekula van, s mindegyik kicsit más sebességgel mozog, ezért a molekulák sebességének leírására átlagokat használnak. Ahogy a matematikában van számtani, négyzetes, mértani és harmonikus közép, a kinetikus gázelméletben is több különböző átlagértékkel kell foglalkozni. A Bunsen-féle kiömlési törvényből levezethető sebesség éppen a gázmolekulák legvalószínűbb sebességével azonos. Ezen kívül létezik még átlagsebesség (v_átl) és négyzetes átlagsebesség (c):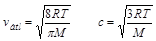

   

8. Habár a molekulák mozgásának átlagsebessége nincs közvetlen kapcsolatban a szélsebességgel, egy megoldó tanulságos és alapjában véve helyes gondolatmenetet vitt végig a 3. kérdés megválaszolására ilyen alapról indulva. Az alapötlet az volt, hogy valójában nem a molekulák mozgásának teljes átlagsebességére van szükség, hanem ennek egy adott irányú komponensére, hiszen az űrhajóból való kiszökésnél csak a zsilipre merőleges irányú sebesség számít. Pitagorasz tételét felhasználva megmutatható, hogy egy adott irányban mérve (nevezzük ezt az irányt x-nek) a molekulák sebességének négyzetes átlaga: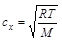

   

   Ezt a c_x értéket kell korrigálni azzal, hogy a föld felszínén nagyobb a nyomás, mint az űrhajóban. A megoldó ezt a korrekciót úgy végezte el, hogy szorzott a két nyomás hányadosával: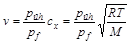

   

   Ez a képlet már nagyon közel van a v-re a feladatszerző által levezetetthez, a különbség az, hogy a korábbiban p_űh/p_f tag is a négyzetgyök alatt szerepel. Számértékben így a megoldó nagyon hasonló értékre jutott az itt megadott 1000 km/h-hoz. A szélsebesség nem különösebben jól definiált fogalom a földfelszínen sem, ezért ez a megoldás erre a részfeladatra maximális pontot kapott.

2013.08.27.