ScienceBits
Lente Gábor blogja
Magaslati légnyomás
KÖZÉPISKOLAI KÉMIAI LAPOK, SZAKMAI

Melyik futballválogatott győzte le 2009-ben világbajnoki selejtezőn a brazil és az argentin csapatot is? Ez a bravúr a világranglistán 58-60. helyezett Bolíviának sikerült (április 1: Bolívia-Argentína 6:1, október 11: Bolívia-Brazília 2:1). Mindkét mérkőzést Bolívia fővárosában, La Paz-ban játszották, amely kb. 3600 méterrel van a tengerszint fölött. A sportokban közismert, hogy nagy tengerszint fölötti magasságban sokkal nehezebb jó teljesítményt nyújtani, mint tengerszinten. Vajon mi lehet ennek az oka?
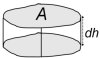
Közismert dolog, hogy a tengerszint fölötti magasság növekedésével a levegő egyre ritkább lesz, így az oxigén koncentrációja is csökken. A kérdés tudományosabb vizsgálatához tételezzük fel, hogy a légnyomás (s így a levegő sűrűségének) ilyen változását kizárólag a levegő saját súlya okozza. Gondolatban képzeljük el egy vékony levegőréteget (1. ábra), amelynek vízszintessel párhuzamosan mért felülete
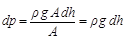
(1)
Ebben a képletben
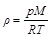
(2)
Ebben a képletben
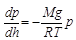
(3)
Tehát a nyomás tengerszint fölötti magassággal való változását leíró függvény olyan tulajdonságú, hogy meredeksége minden pontban kiszámolható a nyomás és egy állandó szorzataként. Ennek a nagyon speciális függvénynek külön neve van a matematikában: exponenciális függvénynek hívják (
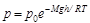
(4)
Ezt a kifejezést barometrikus képletnek is hívják. A sűrűség a 2-es egyenletből közvetlenül adódik:
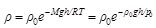
(5)
Természetesen
Próbáljunk meg javítani egy kicsit a megoldáson. Tudjuk, hogy a levegő hőmérséklete a magasság növelésével (legalábbis egy darabig) csökken. Az energiamegmaradás törvényéből kiindulva becsüljük meg, mennyivel. Egy molekulának teljes energiája a mozgási, rezgési és helyzeti energiák összege. Egy mol gáz helyzeti energiáját – a tengerszintet választva vonatkoztatási pontnak – egészen egyszerű kiszámítani (
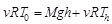
(6)
Itt
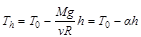
(7)
Itt bevezettük az
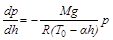
(8)
Hozzáértő emberek ezt a differenciálegyenletet is meg tudják oldani. Ha a kezdeti feltétel az előző esettel azonos (
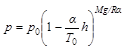
(9)
A 4-es és 9-es képlettel számolt légnyomásokat mutatja be a 2. ábra a tengerszint fölötti magasság függvényében,
Az ábra feltünteti az egyes magasságokban a 7-es egyenlet alapján számolt hőmérsékletet, valamint a tényleges mért (átlagos) nyomást és hőmérsékletet. A 4-es egyenlet felülbecsli, a 9-es pedig jelentősen alulbecsli az egyes magasságokban kísérletileg mért nyomást. Ennek az oka is elég jól látható az ábrából: a hőmérséklet változását egyik egyenlet sem veszi jól figyelembe. A 4-es egyenletnél azt feltételeztük, hogy a hőmérséklet egyáltalán nem változik felfelé haladva, ez természetesen nem igaz. A 7-es egyenlet szerint α értéke 0,0137 K/m, vagyis felfelé a hőmérséklet lineárisan kb. 75 méterenként csökken 1 °C-ot. A nagy utasszállító repülőgépek utazómagasságában, kb. 12000 m-en ezen jóslat szerint -150 °C-nak kellene lennie. Ha valaki emlékszik azonban a repülőgépes élményeire, valójában kívül „csak” -60 °C körüli hideg uralkodik. A tapasztalat az, hogy a légkörben zajló igen összetett folyamatok eredményeként a hőmérsékletcsökkenés valóban közel lineáris, de értéke csak 160 méterenként 1 °C. Az ennek megfelelő
Az ábra elárulja, hogy La Paz tengerszint fölötti magasságában a légnyomás csak kb. 65%-a, így a levegő oxigénkoncentrációja is csak kétharmada a szokásosnak. Egy focimeccs közben a játékosoknak rengeteget kell futniuk, ehhez a vér igen jó oxigénellátása szükséges. A tüdőben az oxigénfelvétel lényegében egyensúlyszerű folyamatban zajlik a hemoglobin (Hb) nevű oxigénszállító fehérjével:
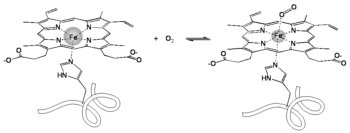
(10)
Így a külső oxigénkoncentráció csökkenésével a vérben a hemoglobinhoz kötött oxigén (HbO2) koncentrációja is csökken, vagyis az izomsejtek nehezebben végeznek munkát.
Hogyan lehetséges, hogy ez a hatás a brazilokat és argentinokat hátrányba hozta az ellenféllel szemben? A bolíviai csapatnak sem lehet más a levegő oxigénkoncentrációja! Az ember szervezete azonban bizonyos mértékig képes alkalmazkodni a nagyobb magasságban lévő a kisebb oxigénkoncentrációhoz több hemoglobin termelésével. Ezzel a 10-es egyenlet egyensúlyát ismét vissza lehet egy kicsit tolni, így a vérben kötött oxigén koncentrációja növekszik. Az ilyen élettani folyamatokhoz azonban hetek szükségesek. Ha viszont valaki eleve ilyen magasságban él, annak a szervezete folyamatosan több hemoglobint tartalmaz. A modern futball vezető csapatai nem engedhetik meg maguknak, hogy egyetlen mérkőzés előtt heteket töltsenek a helyszínen csak azért, hogy hozzászokjanak a körülményekhez. A Nemzetközi Labdarúgószövet-ségben (FIFA) két éve komoly vitát okozott a nagy tengerszint fölötti magasságban fekvő pályák kérdése, de végül is Bolívia megkapta a jogot arra, hogy fővárosában játsszon. Bolívia egyébként a tízcsapatos dél-amerikai selejtezőcsoportban mindössze kilencedik lett, a legtöbb gólt kapta, idegenben (jóval kisebb tengerszint fölötti magasságban) lejátszott kilenc mérkőzéséből nyolcszor vereséget szenvedett és csak egy döntetlent ért el. La Pazban azonban csak Chile, Ecuador és Venezuela tudott nyerni, ezek közül az első két csapat játékosai saját nemzeti bajnokságukban is rendszeresen játszanak nagy tengerszint fölötti magasságban. La Paz városának földrajzi iróniája egyébként, hogy tulajdonképpen völgyben fekszik, a mellette lévő hegyoldalon kialakult külváros neve pedig El Alto (’Magaslat’ spanyolul).
A nagy tengerszint fölötti magasságban kialakuló oxigénhiányos állapotot hegyi betegség vagy magassági betegség néven is ismerik. Az emberi szervezet teljesítőképességének legvégső határa ilyen szempontból a Föld legmagasabb hegye: a Mt. Everest-et kellően hosszú alkalmazkodás után a nagyon jól edzett hegymászók oxigénpalack használata nélkül is meg tudják mászni (mások szerint ostobaság az ember egészségét ilyen célból kockára tenni). A repülőgépek természetesen légmentesen zárhatók, bennük a kintinél jóval nagyobb mesterséges nyomást tartanak fenn, ez általában a kb. 2400 méteres magasságban mérhető légnyomásnak felel meg. A repülőterek megközelítésének utolsó szakaszában sokan érzékelik a légnyomás gyors növekedését fülpattogás formájában. A fül nagyon érzékeny erre, hiszen a hang nem más, mint gyors nyomásváltozás. A mexikóvárosi repülőtéren való leszállások sajátja az ilyen fülpattogás elmaradása: ez a város ugyanis éppen 2400 méterrel van a tengerszint fölött. Mexikóváros sportszempontból is nevezetes hely, mert olimpiai játékokat és labdarúgó világbajnoki döntőt is rendeztek már ott.
Sajnos a repülés története ismer olyan balesetet, amikor a mesterséges nyomást fenntartó rendszert a pilóták elfelejtették bekapcsolni. A Helios légitársaság 522-es járata 2005. augusztus 14-én a ciprusi Larnacaból Athénba tartott volna. Felszállás után a pilóták nem észlelték a hibát, s mire rájöhettek volna, már kómába estek. Az automata pilóta a célig vitte el a gépet, majd Athén közelében addig körözött, amíg el nem fogyott az üzemanyag. Senki nem élte túl a szerencsétlenséget.
A légnyomásváltozás kedvesebb oldalához tartozik az élelmiszeripar egy problémája: jégkrémeket a csomagolás után nem szabad jelentősen más tengerszint fölötti magasságú helyre szállítani. A legtöbb jégkrém belső szerkezetébe ugyanis szándékosan jelentős mennyiségű levegőt zárnak be. Ha a külső légnyomás jelentősen kisebb lesz, akkor „kipukkan” a jégkrém, ha jelentősen nagyobb, akkor összeesik.
Térjünk vissza egy gondolatmenet erejéig az 1. ábrához és képzeljünk el egy ott szereplővel azonos alakú testet, és ne feledkezzünk meg arról sem, hogy a gázokban (és persze a folyadékokban is) a nyomás minden irányba terjed. A test alsó felszínére kicsit nagyobb nyomás hat, mint a felsőre. A nyomáskülönbség által a testre gyakorolt emelőerőt ki is számolhatjuk:
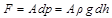
(11)
Emlékezzünk rá, hogy
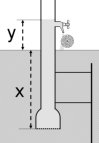
Az 1-es egyenlet nemcsak gázokra, hanem folyadékokra is alkalmazható. A 3. ábrán bemutatott képzeletbeli gép esetében ennek jelentősége van. A gép egy tengerbe mártott cső, amelynek az aljára féligáteresztő hártyát erősítünk. Ezen a hártyán a víz átjut, de a benne oldott só már nem. A tengervíz átlagos NaCl-tartalma 35 g/dm3, vagyis 0,60 mol/dm3. A csőben belül tiszta víz lesz, aminek a sűrűsége kisebb, mint a külső tengervízé. Az
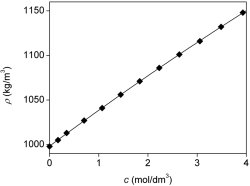
Hol hibás ez az örökmozgó-elképzelés? A sóoldat sűrűsége valóban nagyobb a vízénél. A 4. ábra mutatja be a NaCl-oldatok sűrűségének változását a koncentráció függvényében. A féligáteresztő hártya viszont önmagában is akadályt képez az oldat számára, ezért a nyomás is csökken rajta. Ezt a nyomáscsökkenést ozmózisnyomásként (
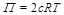
(12)
A 0,60 mol/dm3-es konyhasóoldat ozmózisnyomása 20 °C-on 2,9 MPa (ne felejtsük el, hogy a koncentrációt ide mol/m3 egységben érdemes beírni, hogy Pa-ban kapjuk a nyomást!) sűrűsége 1023 kg/m3, a tiszta vízé 998 kg/m3. A konyhasóoldat és tiszta víz közötti ozmózisnyomás-különbség kiegyenlítéséhez szükséges
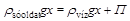
(13)
Ebből a mélységre
Működhetne ez az elképzelés, ha a Föld óceánjai mélyebbek lennének? A vicces az, hogy elvileg valószínűleg működhetne, de persze nem lenne örökmozgó. Ez a gép az időjárási hatások, geológiai folyamatok és az élőlények vízkeverésre fordított energiáját alakítaná át (igen csekély hatékonysággal) munkává. Ha ugyanis nem keveredne a víz, a gravitációs hatásra beálló egyensúlyban a koncentráció, így a sűrűség is lefelé növekedne egy kicsit. Ezt az ülepedési egyensúlynak nevezett jelenséget a modern tudományban a centrifugálás műveleténél fel is használják. Az egyensúly kialakulásának éppen az a feltétele, hogy az oldat ozmózisnyomásának koncentrációváltozás miatti növekedése pontosan kiegyenlítse a hidrosztatikai nyomásnövekedést:
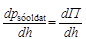
(14)
A 4. ábrában megadott koncentrációfüggést a következő egyenlettel közelítjük:
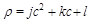
(15)
Az egyenletben szereplő állandók értéke
A 14-es differenciálegyenletet így módosíthatjuk az 1-es, 12-es és 15-ös egyenletek felhasználásával:
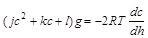
(16)
A negatív előjel annak a következménye, hogy a tengerben mért mélységet negatív tengerszint fölötti magasságként értelmezzük. Ez tehát egy olyan differenciálegyenlet, amelyből a koncentráció mélység szerinti megváltozását lehet kiszámolni. A megoldás elég hosszadalmas, de nem lehetetlen. Persze itt is kell kezdeti feltétel, ez legyen az, hogy a felszínen (
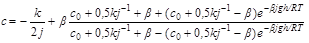
ahol (17)
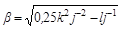
Felmehet-e hát a belső csőben a vízszint a külsőnél magasabbra? Erre a kérdésre első ránézésre nem könnyű válaszolni, hiszen a mélység növekedésével növekvő sókoncentráció miatt a tengervíz sűrűsége is növekszik (méghozzá az elég bonyolult, 17-es képletben leírt függvény szerint), így adott mélységben a nyomást nagyon nehéz kiszámítani. Emellett az is jelentős probléma, hogy ha komolyan vesszük a 17-es egyenletet, akkor már 1500 méteres mélységben elérné a NaCl-koncentráció a 4 mol/dm3-t, ami a telített oldatnak felel meg (ezért ér véget a 4. ábra skálája itt). Emellett az is probléma, hogy a nagy mélységekben uralkodó nagy nyomásokon az oldat mégoly kicsiny összenyomhatósága is jelentős hatással van, amit az eddigi egyenletek nem vesznek figyelembe. Sőt, a hőmérséklet sem egyenletesen 20 °C lefelé haladva.
Le kell hát mondanunk arról, hogy eldöntsük ezt a kérdést? Nem. Csak arról kell lemondanunk, hogy egy adott mélységben kiszámítsuk a pontos nyomást. Van egy viszonylag egyszerű gondolatmenet, amivel bizonyíthatjuk, hogy egyensúlyban nem működhet ez az örökmozgó (sem). Ha éppen a felszínhez érintjük a féligáteresztő hártyát, akkor nyilván nem lesz semennyi tiszta víz a csőben, mert nincs hidrosztatikai nyomáskülönbség. Ahhoz, hogy a cső lefelé nyomásakor bármikor emelkedjék a vízszint belül, szükséges lenne az, hogy a hidrosztatikai nyomás kis megváltozása nagyobb legyen az ozmózisnyomás megváltozásánál. Ez a két megváltozás egyensúlyban viszont a 14-es egyenlet miatt mindig egyenlő.
![]() 2010.01.13.
2010.01.13.
