ScienceBits
Lente Gábor blogja
Sugárzó bizmut
KÖZÉPISKOLAI KÉMIAI LAPOK, SZAKMAI

Bizmut kristály
A tudomány hosszú ideig a bizmutnak a természetben előforduló egyetlen, 209-es izotópját tartotta a legnagyobb tömegszámú stabil atommagnak. 2003-ban ez a kitüntető cím azonban az ólom 208-ra szállt át, mert a jelenlegi csúcstechnológiát képviselő műszerekkel sikerült kimutatni, hogy a 209Bi valójában nagyon lassú radioaktív alfa-bomláson megy át. A detektálás fő nehézsége az volt, hogy a bomlások nagyon ritkák, ezért a hagyományos módszerekkel nem mutathatók ki. A siker kulcsa egy újonnan készített eszköz, a szcintillációs bolométer volt. Ez két, egy évszázadnál is régebben ismert eszközt egyesít.
A szcintillációs detektorokat radioaktív részecskék kimutatására használják. Néhány szilárd anyagban a töltéssel rendelkező, nagy energiájú részecskék elnyelődése apró felvillanásokat okoz. A felvillanások megszámlálásával a radioaktív sugárzás intenzitása megbecsülhető. Ilyen elven működött Ernest Rutherford (1871-1934) híres kísérletében az aranyfólián áthaladó alfa-részecskék kimutatására használt cink-szulfid-ernyő.
A bolométer elektromágneses sugárzás energiájának mérésére alkamas eszköz, Samuel Pierpont Langley (1834-1906) csillagász találta fel. Működésének lényege, hogy egy abszolút nulla fok közelébe hűtött szilárd testben (az abszorberben) az elnyelődő sugárzás által okozott hőmérsékletemelkedést mérik. Természetesen ez csak egy nagyon költséges hűtőrendszer üzemeltetésével lehetséges, ezért a legtöbb esetben a bolométert ritkán használják, és akkor is csak olyan hullámhossztartományú (200 μm – 1 mm) sugárzás intenzitásának mérésére, amelyre nem ismeretes érzékenyebb detektor.
E két eszközt egyesítették mintegy 20 éve nagyon ritka radioaktív bomlások tanulmányozására. A 209Bi alfa-bomlásának kimutatását az a felismerés tette lehetővé, hogy a Bi4Ge3O12 kettős oxid kristályai jól szcintillálnak, és bolométeranyagnak is alkalmasok. Egy ilyen bolométer fényképét és elvi sémáját mutatja be az 1. ábra. Az eszköz átmérője és magassága egyaránt 20 mm, s egy fényvisszaverő ezüstbevonattal ellátott kamrában van, amelyet egy 0,020 K hőmérsékletű speciális hűtőbe helyeznek. Az elvi ábrán bal oldalon lévő, 25 mm átmérőjű és 0,10 mm vastag Ge-lemezben a ráeső fény fotoáramot kelt, így segítségével a felvillanásokat észlelni lehet. A jobb oldalon lévő, speciálisan adalékolt Ge-darab ellenállásán keresztül a hőmérsékletre lehet következtetni. Így aztán az eszközzel a benne elnyelődő ionizáló részecskék számát és energiáját is meg lehet határozni. A szcintillációs bolométert minden külső hatástól a lehető legjobban el kell szigetelni, hogy a természetes háttérsugárzás a lehető legkevésbé zavarja a méréseket. A 209Bi a kristály anyagában van, ezért radioaktív bomlásai magában a kristályban történnek, és a szcintillációs detektálás nagy hatékonysága biztosítja azt is, hogy egyetlen egy bizmutatom sem bomolhat el észrevétlenül. A kísérlet során azt tapasztalták, hogy kb. öt nap alatt több tucat, külső hatásokkal nem értelmezhető bomlás történt, amelyeknél az ionizáló részecske energiája 503 fJ (5,03∙10-13 J) volt.
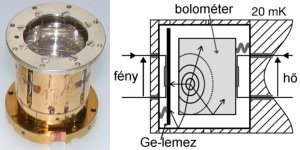
A bizmut-209 radioaktivitásának kimutatására
használt szcintillációs bolométer fényképe és
elvi sémája
Hogyan lehet ellenőrizni, hogy ez lehet a Bi-209 alfa-bomlásának következménye? Tömegspektrométerrel egyes izotópok relatív atomtömegét igen nagy pontossággal meg lehet határozni: a 209Bi-é 208,980374, a 205Tl-é 204,974401, a 4He-é pedig 4,00260324. Ha a Bi-209 valóban alfa-bomláson megy át, akkor ennek egyenlete:
A keletkező 205Tl és 4He tömegének összege 208,9770042, vagyis kisebb, mint a kiindulási 209Bi tömege. A különbséget ( Vagyis a várt bomláshoz tartozó energifelaszabadulás éppen megegyezik a kísérletileg tapasztalttal. A 209Bi felezési idejét is ki lehetett számolni a mért adatok alapján. A 45,7 g tömegű Bi4Ge3O12 bolométerben 100 óra alatt 41 bomlást regisztráltak. A kristályban lévő Bi-209 atomok száma:
A bomlási állandó ilyen körülmények között kiszámolható az elbomlott atomok hányada és az eltelt idő osztásával:
A felezési idő pedig:
A francia kutatócsoport készített egy másik, 91,2 g tömegű szcintillációs bolométert is. Ebben 114 óra alatt 77 bomlást detektáltak. Az összes adatot együtt kiértékelve a 209Bi felezési idejére (1,9 ± 0,02)∙1019 év adódott. Ez a felezési idő a világegyetem ma ismert koránál kilenc nagyságrenddel nagyobb, vagyis annak egymilliárdszorosa. Azt gondolhatnánk, hogy hosszabbat már elvileg is lehetetlen mérni. Azonban ez sem teljesen így van. Az 1. táblázat a ma ismert, kivételesen hosszú (1015 évnél nagyobb) felezési idejű izotópokat tünteti fel. Látható, hogy a 128Te a csúcstartó, felezési ideje még kb. 5 nagyságrenddel nagyobb, mint a 209Bi-é. A természetes tellúrban a 128Te gyakorisága csak 31,7%, így a radioaktivitás felfedezése óta eltelt bő egy évszázad alatt egy nagynak elképzelt, 1 kg tömegű, tiszta tellúrból álló mintában nagyjából 50 db 128Te-bomlás történt volna. Hogyan lehet hát meghatározni a felezési idejét? Az eljárás kulcsa az, hogy a kísérletet nem kell feltétlenül tudósoknak elkezdeniük: néhány szerencsés esetben a természet maga gondoskodott erről. A 130Te β--bomláson megy át, amelynek közvetlen terméke a 130I, amely gyorsan, 12 óra felezési idővel stabil 130Xe-á alakul. Ismeretes néhány tellúrt nagy mennyiségben tartalmazó ásvány, pl. a tellurobizmutit (Bi2Te3), amelyben a gázzárványok összetételét tömegspektrometriás módszerrel elemezni lehet.
Az 1. táblázatban megadott szám több hasonló kísérlet átlagából származik, és a ma legmegbízhatóbbnak tekintett adatot jelenti. A 128Te felezési idejét pedig hasonló gázzárványokban lévő 128Xe és 130Xe mennyisége alapján számították ki.
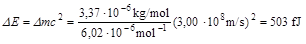
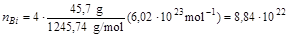
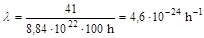
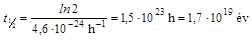
Kivételesen hosszú felezési idejű radioaktív izotópok
izotóp
48Ca
50V
76Ge
82Se
96Zr
100Mo
113Cd
116Cd
felezési idő (év)
5,3∙1019
1,5∙1017
1,6∙1021
9,7∙1019
2,4∙1019
8,5∙1018
7,7∙1015
3,0∙1019
128Te
130Te
144Nd
148Sm
150Nd
174Hf
180W
186Os
209Bi
2,2∙1024
7,9∙1020
3,3∙1015
7∙1015
6,7∙1018
2,0∙1015
1,8∙1018
2,0∙1015
1,9∙1019
Ismeretes, hogy bizonyos körülmények között ezen kőzetbe zárt gázok még földtörténeti korok alatt sem távoznak el. Egy ilyen típusú kőzetből származó, 210 mg tömegű Bi2Te3 minta zárványaiban 29,8 amol 130Xe (1 amol = 1 attomol = 10-18 mol) és 56,9 amol 132Xe volt. A minta közelében talált, tellúrt nem tartalmazó kvarcminta 38,2 mg-jában a 132Xe anyagmennyisége 51,5 amol, a 130Xe-é pedig 7,81 amol volt. A kvarcban csak a kristályosodás kezdetekor belezárt levegő miatt van Xe, izotópjainak aránya jól egyezik a mai levegőben mérhető 132Xe:130Xe = 6,6:1 aránnyal. A Bi2Te3 mintában a 130Xe két forrásból származik: a bezárt levegőből és a 130Te bomlásából. A levegőből származó mennyiségnek 56,9∙7,81/51,5 = 8,63 amol-nak kell lennie, így a radioaktív bomlás során 29,8 - 8,63 = 21,2 amol keletkezett. A 210 mg Bi2Te3 mintában összesen 787 μmol Te van, a 130Te gyakorisága pedig 34,08 %, vagyis a 130Te anyagmennyisége 268 μmol. Most már csak az ásványok keletkezésének idejét kellene ismerni a 130Te felezési idejének a meghatározásához. Ehhez egy másik nemesgáz, az Ar kőzetekben mért mennyiségét lehet felhasználni. A vizsgált kőzetben találtak biotit nevű, K(Mg,Fe)3AlSi3O10(F,OH)2 általános képletű ásványt is. A 40K izotópból 1,3∙109 év felezési idővel, β+-bomlással 40Ar keletkezik. Így az Ar-zárványok mérése alapján meg lehetett határozni, hogy az ásvány 93 millió éve keletkezett. Tehát a 130Te felezési ideje:
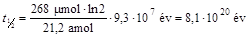
 2009.01.07.
2009.01.07.
